
However, the Weiss zone law is more general, and can be shown to work for all crystal systems, to determine if a direction lies in a plane.įrom the Weiss zone law the following rule can be derived: Indeed, in a cubic system, the scalar product can be used to determine the angle between a direction and a plane. In a cubic system this is exactly analogous to taking the scalar product of the direction and the plane normal, so that if they are perpendicular, the angle between them, θ, is 90°, then cosθ = 0, and the direction lies in the plane. If the direction lies in the plane ( hkl), then: Your browser does not support the video tag. The normal to the (100) plane in this case is A simple example is the case of in the (100) plane of a hexagonal system, where the direction is actually at 120° (or 60° ) to the plane. This is not always the case, as directions in a crystal are written in terms of the lattice vectors, which are not necessarily orthogonal, or of the same magnitude. It may seem, after considering cubic systems, that any lattice plane ( hkl) has a normal direction. They are written with "square" brackets:Ī number of crystallographic directions can also be symmetrically equivalent, in which case a set of directions are written with "triangular" brackets: These are effectively vectors written in terms of multiples of the lattice vectors a, b, and c. That is why it useful to consider the equivalent (010) set of planes.ĭirections in the crystal can be labelled in a similar way. These planes all "look" the same and are related to each other by the symmetry elements present in a cube, hence their different indices depend only on the way the unit cell axes are defined. When referring to a set of planes related by symmetry, then "curly" brackets are used: When referring to a specific plane, "round" brackets are used: In crystallography there are conventions as to how the indices of planes and directions are written.
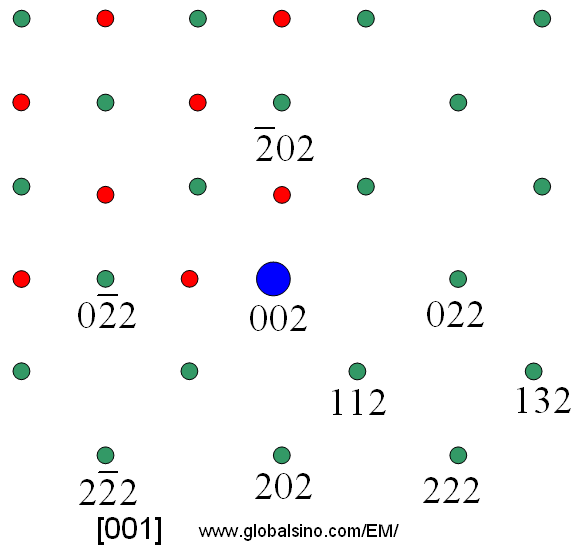
Indexed single crystal diffraction pattern bcc how to#
How to draw a lattice plane Bracket Conventions The diagram shows the trace of the (2 13) Lattice planes can be represented by showing the trace of the planes on theįaces of one or more unit cells. Click "Start" to begin and use the buttons at the bottom right to navigate through the pages.
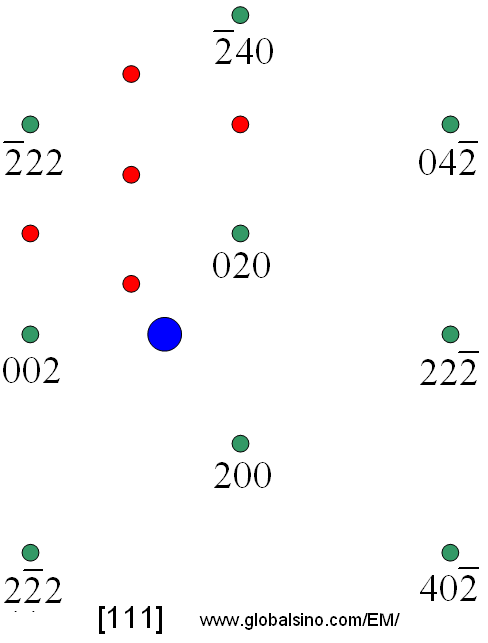
This animation explains the relationships between parallel planes and their indices. Click "Start" to begin each animation, and then navigate through the pages using the buttons at the bottom right. The next three animations take you through the basics of how to index a plane. These indices are useful in understanding many phenomena in materials science, such as explaining the shapes of single crystals, the form of some materials' microstructure, the interpretation of X-ray diffraction patterns, and the movement of a dislocation, which may determine the mechanical properties of the material. They were developed by William Hallowes Miller. Miller Indices are a method of describing the orientation of a plane or set of planes within a lattice in relation to the unit cell. You should understand the concepts of vectors and planes in mathematics. You might also like to look at the TLP on Atomic Scale Structure of Materials. Lattice, unit cell, crystal axes, vrystal system and the variations, primitive, FCC, BCC which make up the Bravais lattice. Be aware of how knowledge of lattice planes and their Miller indices can help to understand other concepts in materials science.Be able to visualise and draw a plane when given its Miller indices.Be able to determine the Miller indices of a plane from its intercepts with the edges of the unit cell.Understand the concept of a lattice plane.$$\sin\theta=\frac are present for the primitave cubic, $h+k+l=$ odd are absent in bcc and for face centred lattices for a reflection to be present h, k, l are all odd or all even.


 0 kommentar(er)
0 kommentar(er)
